SIFT
SIFT 尺度不变特征变换
https://www.cnblogs.com/wangguchangqing/p/4853263.html
如何知道两张图片包含相同的信息?
下图是第一张图片的某个点映射到第二个图片的具有相同语义的点

1. 建立高斯差分金字塔
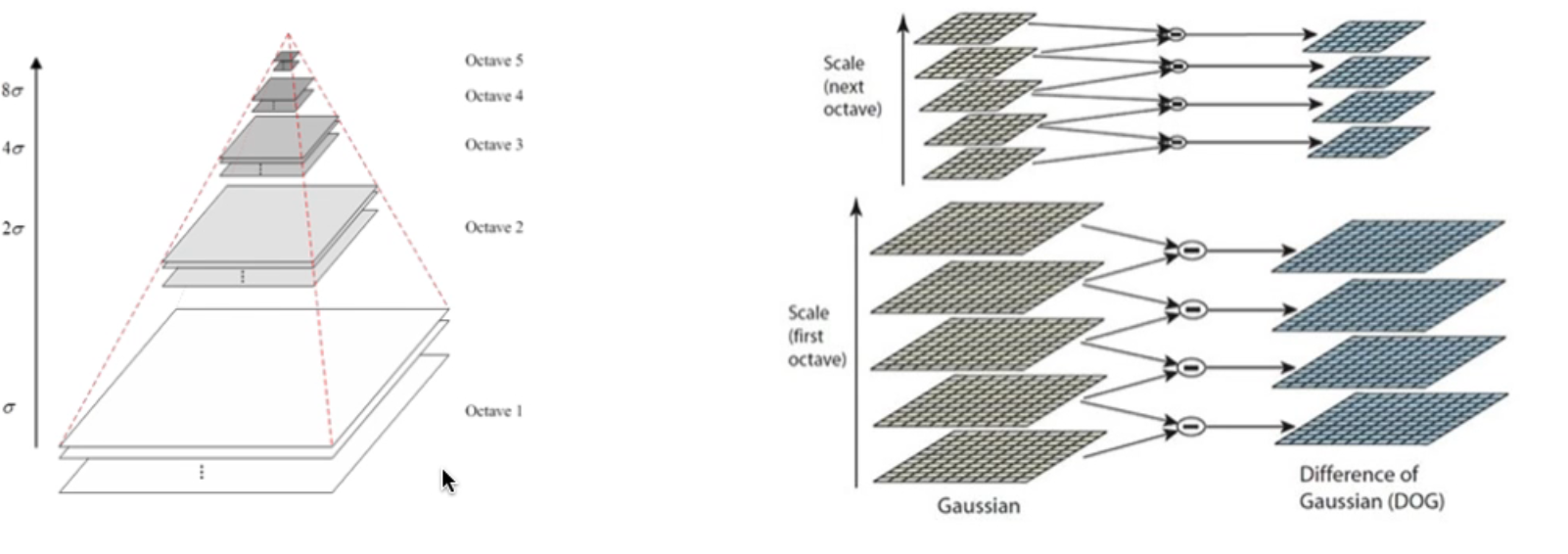
左图
- 同样大小的图片为一组,每一组图片有很多层
- 第一组图片使用不同尺度()的高斯核进行卷积得到的
- 模拟近大远小,高斯核的作用:近处清晰远处模糊
- 第二组图片是第一组图片进行降采样得到
- 其余组以此类推
右图
-
在同一组内两层图片相减得到Difference of Gaussian(DOG), 高斯差分金字塔
-
论文中给出的建议值:
-
- O是应该有多少组
- M, N是原图片的宽和高
-
-
每组有S层
-
n是希望从多少张图片中提取特征
比如五张图片差分后得到4张,然后因为要在尺度空间中求极值,所以需要求导,最上和最下的图片无法求导,4 - 2 = 2
-
-
如何确定?
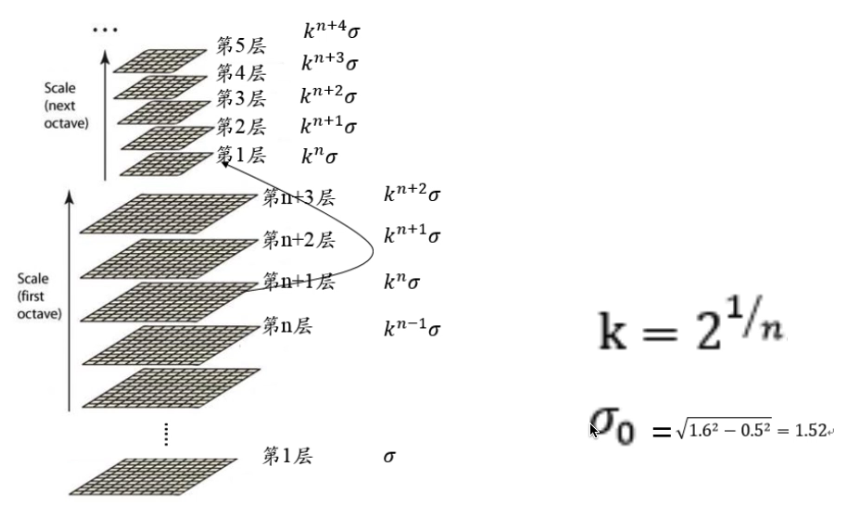
- 第一组第一层用, 第一组第二层用…
- 第二组第一层用第一组的倒数第三层, 带入后凑2
- 0.5 是经验值, 1.6是希望得到的效果,高斯分布的方差和
2. 极值点的精确定位
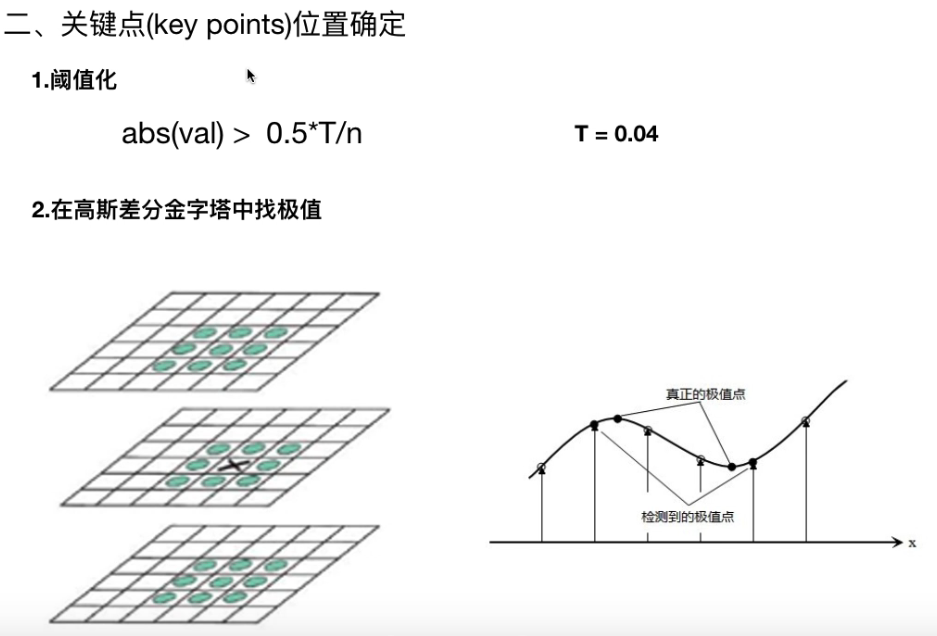
- 关键点就是有稳定性质、不会丢失信息的点, 通常是极值点
- 原来的极值仅在图片的x、y轴,现在和上下左右的26个点作比较
- 阈值化:如果绝对值小于很有可能是噪声
- 检测到的极值点很有可能不是真正的极值点,所以需要进一步找到亚像素级别的真正的极值点
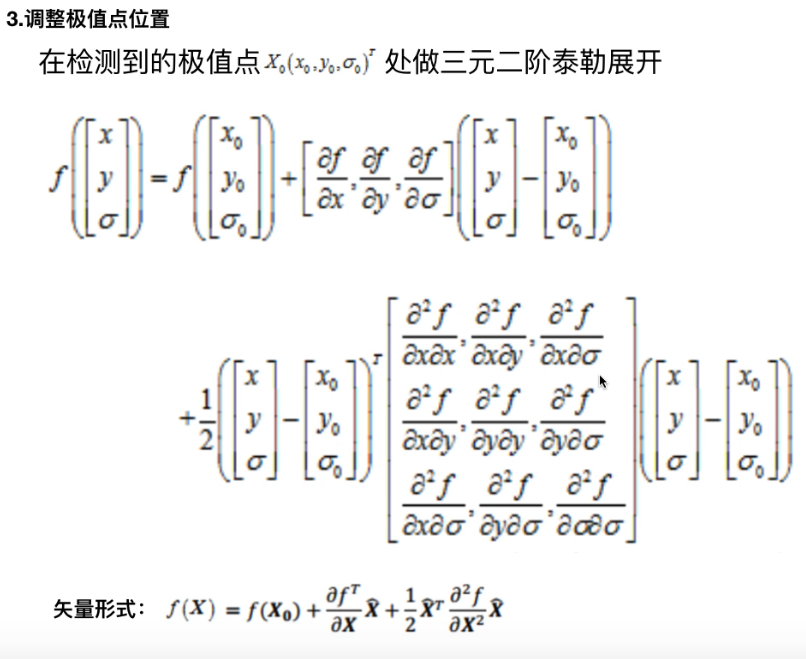
- 极值点应该在检测到的点附近,在附近做泰勒展开


-
对比度低,很有可能是噪声
-
Hessian矩阵可以描述曲线局部的曲率,希望两个方向的曲率比较接近,否则有可能是边缘
-
Hessian矩阵的曲率和特征值成正比,不算特征值,使用迹和行列式计算
-
Det(H)小于零,曲率异号,不满足条件
-
我们希望, ,这个式子单调递增,所以两个条件等价
实际求导使用有限差分求导法,即相邻点做差近似
-
3. 为关键点赋予方向
-
上面已经求出了亚像素的极值,可能落在了两个层之间,选择比较近的层
-
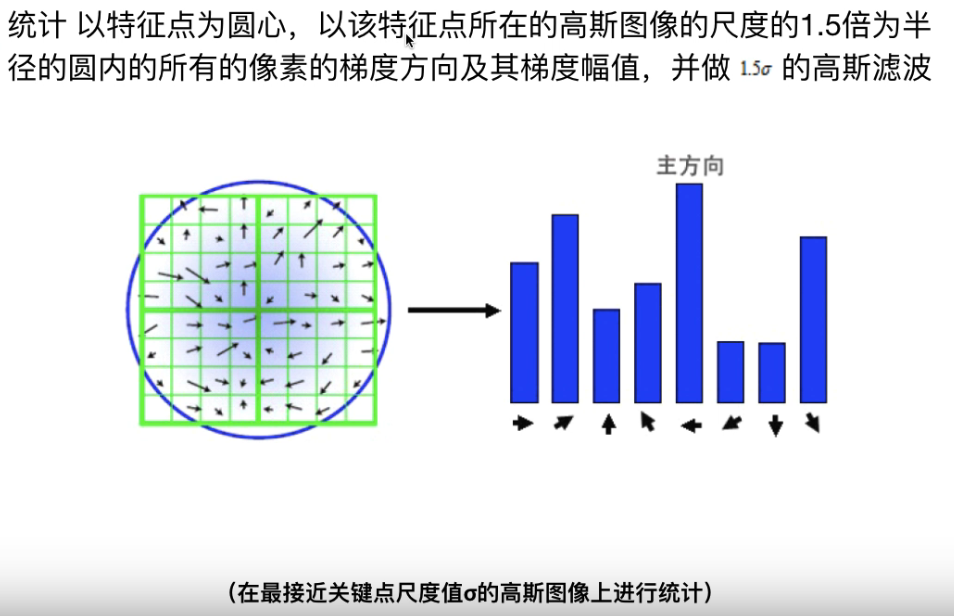
然后以特征点为圆心,把落在该圆内的所有像素根据梯度方向分成八个方向
-
高斯滤波平滑,中间权重大,四周权重小
-
主方向是最后投票结果最大的方向
如果另外一个方向大于比如说主方向的80%,就可以称为一个辅方向(实际作为两个特征点处理)
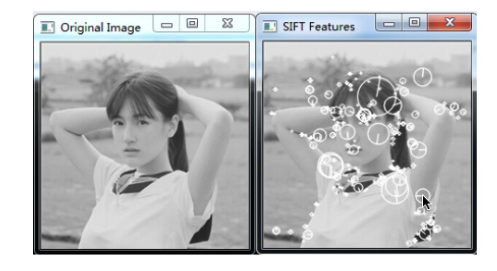
- 圈中心是特征点
- 圈的大小是特征的大小
- 圈中的线是主方向
4. 构建关键点描述符
前面描述了找到一张图片关键点的方法。在实际中我们要找到两张图片的关键点并把它们对应起来,通过构建关键点描述符实现。
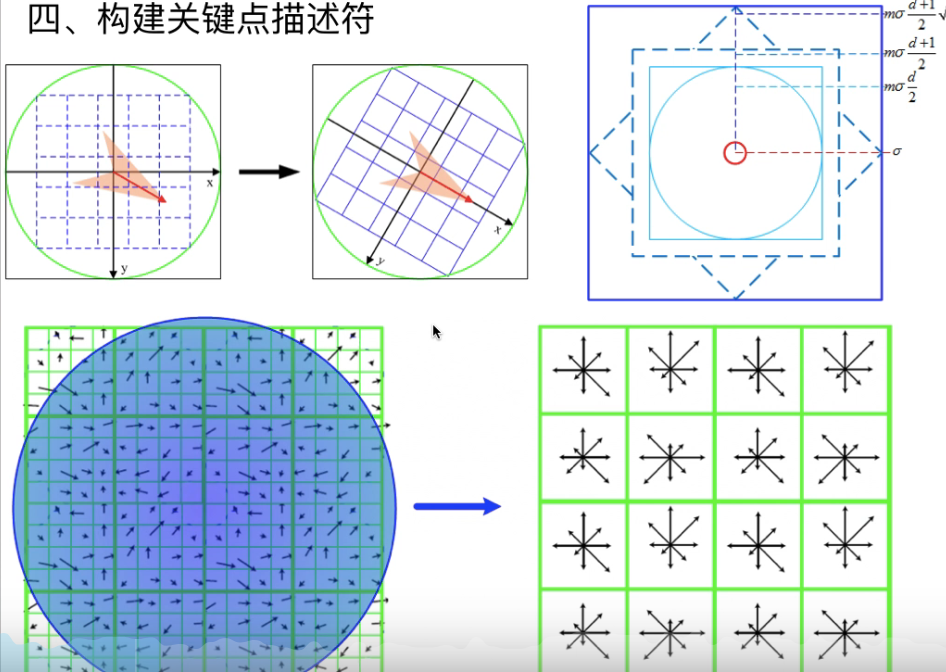
- 描述符是128维的向量
- 把关键点周围分成很多小的子区域,每个子区域又包含了很多像素
- 在每个子区域统计八个方向的梯度(每个子区域8个值)总共8 * 16个值,按顺序写出来就得到了关键点描述符的向量
- 如何划分子区域?
- 首先把周围旋转到主方向上(我们希望sift具有旋转不变性)
- m=3, d=4(横竖多少个子区域)
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
