DiffPool

Hierarchical Graph Representation Learning

Abstract

1. However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs.
2. DIFFPOOL, a diferentiable graph pooling module that can generate hierarchical representations of graphs and can be combined with various GNN architectures.

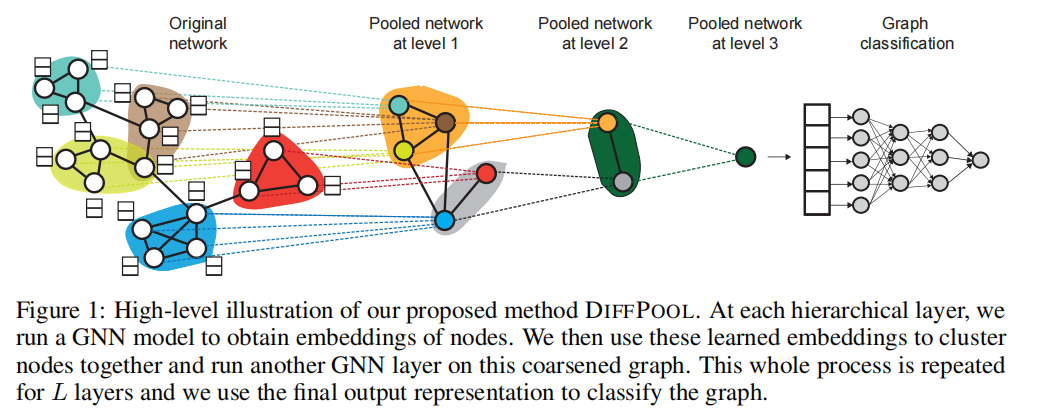
• the input nodes at the layer $l$ GNN module correspond to the clusters learned at the layer $l - 1$​ GNN module.

1. Introduction

1. This lack of hierarchical structure is especially problematic for the task of graph classifification, where the goal is to predict
   the label associated with an entire graph.

   traditional globally pool such as summation or network ignores any hierarchical structure that might be present in the graph.

3. Proposed Method

3.1 Preliminaries

1. $G = (A, F)$

   • $A\in \{0, 1\}^{n\times n}$ is the adjacency matrix
   • $F\in \{R ^{n\times d}\}$ is the node feature matrix assuming each node has d features.

2. Graph neural networks

   general “message-passing” architecture:

   $$H^{(k)}=M\left(A, H^{(k-1)} ; \theta^{(k)}\right)$$

   • $H^{(k)}\in R ^{n\times d}$ are the node embeddings computed after k steps of GNN
   • $M$ : message propagation function
   • $H^{(0)}$ are initialized with $F$

3. A full GNN module will run K iterations to generate the final output node embeddings $Z=H^{(K)} \in R^{n\times d}$​

   For, simplicity, use $Z=GNN(A,X)$ to denote an arbitrary GNN module.

3.2 Differentiable Pooling

Pooling with an assignment matrix

1. $S^{(l)} \in R^{(n_l \times n_{l+ 1})}$

   • Each row of $S^{l}$ corresponds to one at the $n_l$ nodes at layer l
   • Each column corresponds to one at the $n_{l+1}$ nodes at layer l+1.

2. DIFFPOOL layer

   $$\left(A^{(l+1)}, X^{(l+1)}\right)=\operatorname{DiFFPOOL}\left(A^{(l)}, Z^{(l)}\right)$$

   $$\begin{aligned} &X^{(l+1)}=S^{(l)^{T}} Z^{(l)} \in \mathbb{R}^{n_{l+1} \times d} \\ &A^{(l+1)}=S^{(l)^{T}} A^{(l)} S^{(l)} \in \mathbb{R}^{n_{l+1} \times n_{l+1}} \end{aligned}$$

Learning the assignment matrix

• use a standard GNN module to generate Z:

$$Z^{(l)}=\mathrm{GNN}_{l, \text { embed }}\left(A^{(l)}, X^{(l)}\right)$$

• generate an assignment matrix:

  $$S^{(l)}=\operatorname{softmax}\left(\mathrm{GNN}_{l, \text { pool }}\left(A^{(l)}, X^{(l)}\right)\right)$$

  • softmax function is applied in a row-wise fashion
  • the output dimension of $GNN_{l,pool}$ 是超参数

• Note that these two GNNs consume the same input data but have distinct parameterizations and play

  separate roles:

  • The embedding GNN generates new embeddings for the input nodes at this layer,

  • while the pooling GNN generates a probabilistic assignment of the input nodes to $n_{l+1}$​ clusters.

Permutation invariance

in order to be useful for graph classifification, the pooling layer should be invariant under node permutations.

For DIFFPOOL we get the following positive result, which shows that any deep GNN model based on DIFFPOOL is permutation invariant.

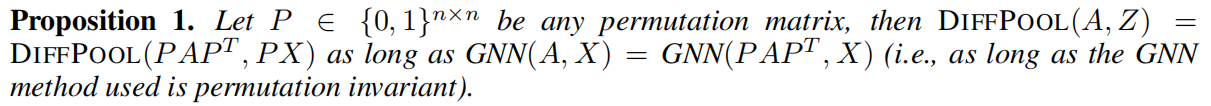
3.3 Auxiliary Link Prediction Objective and Entropy Regularization

注意到在更新A的时候非凸，可能回落到局部极值：

1. at each layer $l$​, minimize

   $$L_{\mathrm{LP}}=\left\|A^{(l)}, S^{(l)} S^{(l)^{T}}\right\|_{F}$$

2. the output cluster assignment for each node should generally be close to a one-hot vector, therefore we regularize the entropy of the cluster assignment by minimizing:

   $$L_E = \frac{1}{n} \sum_{i=1}^n H(S_i)$$

   • H denotes the entropy function
   • $S_i$ is the i-th row of S.

4. Experiment

sensitivity of the pre-defined Maximum Number of Clusters:

• With larger C, the pooling GNN can model more complex hierarchical structure.

  trade off!

  • very large C results in more noise and less efficiency.