Harris角点

图像特征类型

• A和B处于平坦区域，没有什么确切的特征，它们所在的位置有很多种可能；
• C和D要相对简单一些，它们是建筑物的边缘，我们可以找到一个大致的位置，但是要定位到精确的位置仍然很难。所以边缘是更好的特征，但还不够好。
• E和F是建筑的一些角落，可以很容易地发现它们的位置，因为对于建筑物角落这个图像片段，我们不管朝哪个方向移动，这个片段看起来都会不一样。

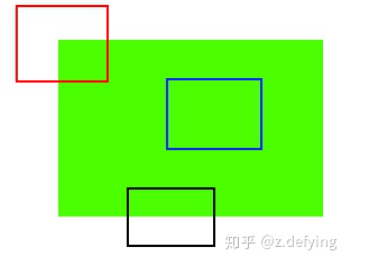
• 蓝色矩形表示一个平坦区域，在各方向移动，窗口内像素值没有变化；
• 黑色矩形表示一个边缘特征（Edges），如果沿着垂直方向移动(梯度方向)，像素值会发生改变；如果沿着边缘移动(平行于边缘) ，像素值不会发生变化；
• 对于红色矩形框来说，它是一个角（Corners），不管你把它朝哪个方向移动，像素值都会发生很大变化。

图像特征提供了图像丰富的信息。角点特征是图像中较好的特征，比边缘特征更好地用于定位。

在图像的所有区域中，那些在所有方向上做微小移动，像素值变化都很大的区域，就是角点特征所在的区域。

Harris 角点检测器

角点是两条边缘的交点，它表示两条边方向改变的地方，所以角点在任意一个方向上做微小移动，都会引起该区域的梯度图的方向和幅值发生很大变化。

也就是一阶导数(即灰度图的梯度)中的局部最大所对应的像素点就是角点。

这样就可以将 Harris 角点检测算法分为以下三步：

1. 当窗口（小的图像片段）同时向 x 和 y 两个方向移动时，计算窗口内部的像素值变化量$E(u,v)$；

   • 

   • 

     

2. 对于每个窗口，都计算其对应的一个角点响应函数 R；

   • 计算每个窗口对应的得分（角点响应函数R）

     $$R = det(M) - k(trace(M))^2$$

     1. $det(M)=\lambda_1 \lambda_2$
     2. $trace(M)=\lambda_1 + \lambda_2$
     3. k是一个经验常数， 在范围(0.04, 0.06)之间

3. 然后对该函数进行阈值处理，如果 R > threshold，表示该窗口对应一个角点特征。

   根据 R 的值，将这个窗口所在的区域划分为平面、边缘或角点。为了得到最优的角点，我们还可以使用非极大值抑制。

   

​

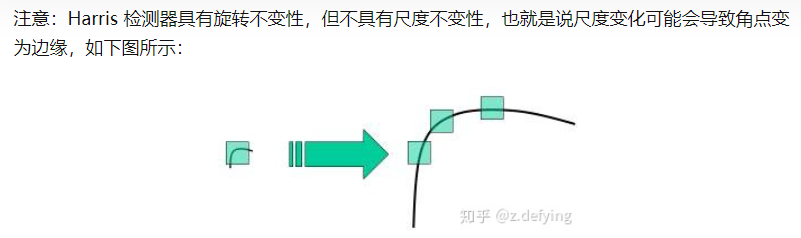
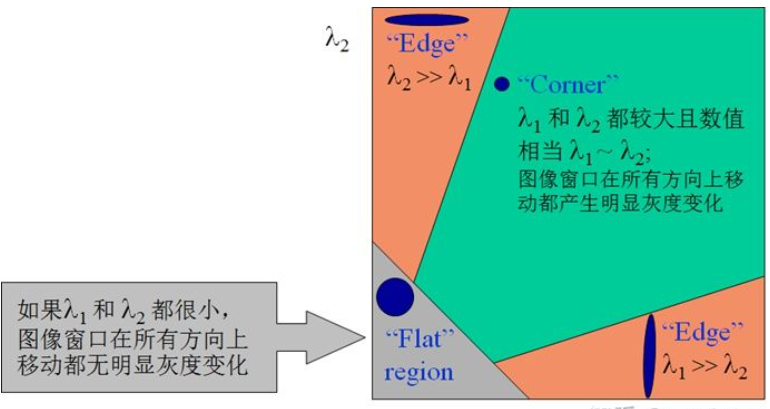
Harris角点检测的结果就是带有这些分数R的灰度图像，设定一个阈值，分数大于这个阈值的像素就对应角点。

Shi-Tomasi 角点检测器

由于 Harris 角点检测算法的稳定性和 k 值有关，而 k 是个经验值，不好设定最佳值。

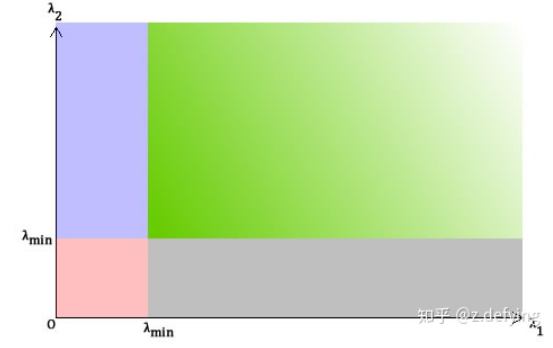
Shi-Tomasi 发现，角点的稳定性其实和矩阵 M 的较小特征值有关，于是直接用较小的那个特征值作为分数。这样就不用调整k值了。

所以 Shi-Tomasi 将分数公式改为如下形式：

$$R = min(\lambda_1, \lambda_2)$$

和Harris一样，如果该分数大于设定的阈值，我们就认为它是一个角点。